Gráfico da evolução temporal do coronavírus – Atualização de 23.03.2020
A epidemia do COVID-19 apresenta no dia de hoje mais de 370.000 casos confirmados ao redor do mundo. Na sua grande maioria, no início da epidemia os países tiveram crescimento exponencial.
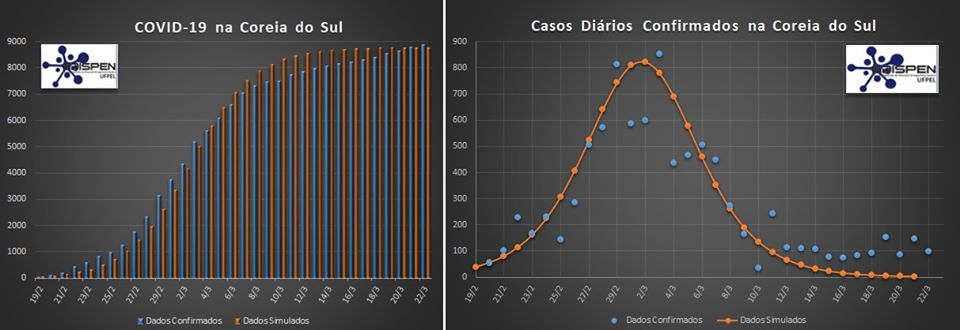O primeiro gráfico apresenta os dados da epidemia para a Coreia do Sul. Pode-se perceber que, com uma rápida atuação de todos, governo e população, é possível conter o vírus. No lado esquerdo do gráfico podemos notar que no dia 27/02 temos o ponto de inflexão da curva, a partir do qual o crescimento da epidemia inicia a diminuir. Temos uma estabilidade no número de casos confirmados a partir do dia 10/3, menos de um mês após a confirmação do caso de número 50. No lado direito do gráfico temos o número de casos que foram confirmados dia a dia, sendo que este número inicia a diminuir depois do dia 02/03. Teoricamente podemos reproduzir a curva da Coreia do Sul ficando em casa.
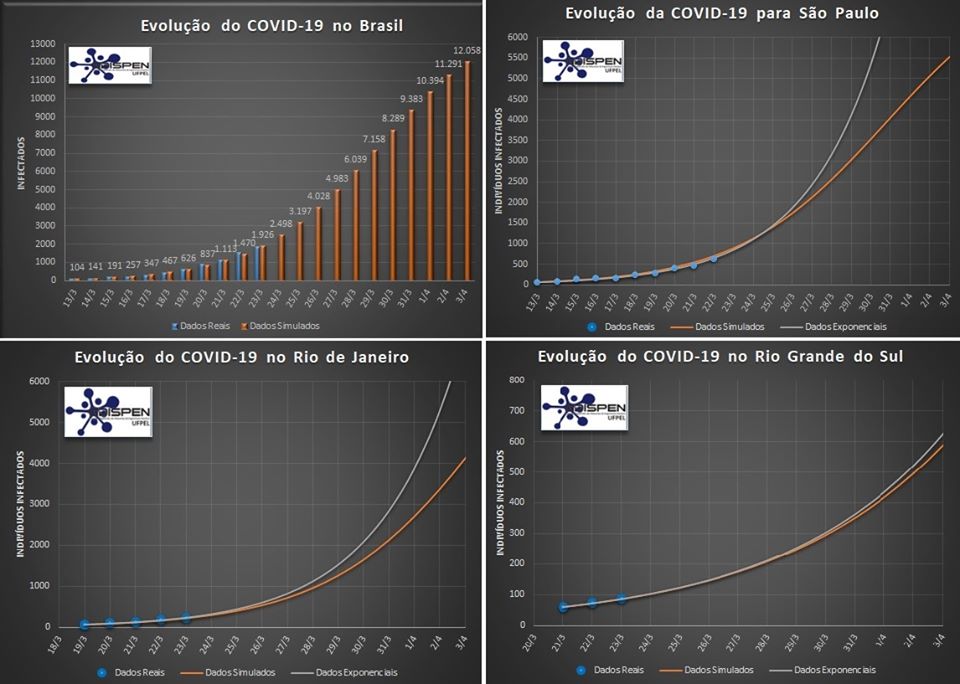
No segundo gráfico temos uma atualização dos dados reais da epidemia para o Brasil e uma previsão do que esperamos para os próximos dias. Para os estados de SP, RJ e RS apresentamos uma previsão do que pode acontecer nos próximos dias. Utilizamos os dados a partir da confirmação do caso 50. Como ainda temos poucos dados, plotamos uma estimativa pelo modelo matemático e por um ajuste exponencial. Note que o ajuste exponencial não é adequado para a previsão de dados pois esta cresce infinitamente. Assim que tivermos mais dados será possível melhorar esta estimativa.
Informações sobre a pesquisa e os pesquisadores envolvidos:
Os pesquisadores do laboratório GDISPEN (Grupo de Dispersão de Poluentes & Engenharia Nuclear) da Universidade Federal de Pelotas (UFPel), Glênio Aguiar Gonçalves, Régis Sperotto de Quadros e Daniela Buske, preocupados com a evolução do coronavírus no Brasil, publicarão diariamente gráficos das curvas da evolução temporal do COVID-19. Para tanto estão sendo utilizados dados da Universidade John Hopkins (EUA), da Wikipedia e do Ministério da Saúde do Brasil. Os dados reais são comparados com uma combinação de modelos matemáticos para epidemias, conhecidos na literatura como modelo SIR e t-norma do mínimo. Serão apresentadas simulações para diversos países, para o Brasil e seus estados, dando ênfase para o estado do Rio Grande do Sul e para a cidade de Pelotas. Este estudo tem objetivo puramente acadêmico e científico, mostrando a grande aplicabilidade da modelagem matemática em problemas reais.
Os docentes do GDISPEN são professores do Departamento de Matemática e Estatística (DME) do Instituto de Física e Matemática (IFM) da UFPel. Os três pesquisadores são doutores e participam do Programa de Pós-Graduação em Modelagem Matemática (PPGMMat) e a Dra. Daniela Buske também participa do Programa de Pós-Graduação em Ciências Ambientais (PPGCAmb) e é bolsista de produtividade do CNPQ.
